Java实现美丽的分形_JAVA

您所在的位置：程序员俱乐部 > 编程开发 > JAVA > Java实现美丽的分形

Java实现美丽的分形

2013/11/29 3:29:54 尧尧1975417219 程序员俱乐部我要评论(0)

摘要：一谈到分形，我就来劲，看到各种美丽的分形图案，我就特别欣喜，所以，我常常到各大网站浏览各种分形图。据说，很多人学计算机语言都是从各种画图开始的，因为常常被美丽的图形所吸引，就会慢慢喜欢上原本比较枯燥编程，我就是那么一个人。之前吧，我对Java学习并没有那么大的兴趣，自从听了分形这个内容以后，我就慢慢的喜欢上了编程，当我独自把柯赫曲线做出来以后，我对编程的喜好就一发不可收拾，现在只要有时间，我就会打开电脑，编写自己喜欢的东西。制作一个分形并不是一件简单的事，需要对递归函数有比较深刻的认识
标签：实现 Java 美丽

    一谈到分形，我就来劲，看到各种美丽的分形图案，我就特别欣喜，所以，我常常到各大网站浏览各种分形图。据说，很多人学计算机语言都是从各种画图开始的，因为常常被美丽的图形所吸引，就会慢慢喜欢上原本比较枯燥编程，我就是那么一个人。之前吧，我对Java学习并没有那么大的兴趣，自从听了分形这个内容以后，我就慢慢的喜欢上了编程，当我独自把柯赫曲线做出来以后，我对编程的喜好就一发不可收拾，现在只要有时间，我就会打开电脑，编写自己喜欢的东西。
   制作一个分形并不是一件简单的事，需要对递归函数有比较深刻的认识，最重要的是要有一定的数学功底，因为在制作中需要计算很多的坐标，一不小心就会出错。之前在做毕达格拉斯树的时候就是因为坐标计算错误，做了一下午都没有没有做出来。后面通过我一步步的检查大概检查了一个小时才发现第二个点坐标计算错误，一个坐标的计算就花了我一下午的时间，所以说，学计算机数学很重要，所以说是“数学是计算机之父”这句话一点都没错。
   其实，这次不怎么想把自己做的分形放到博客上的，因为做的不太好，所以不想丢脸。但是东哥这周要我们写一个有关分形的博客，没办法，丑媳妇总得见公婆，就把之前做的几个不太好看的分形图给大家献丑献丑了。这次总共做了7个分形图，接下来就告诉大家我是怎么实现这七个图形的。

一、首先给大家介绍第一个分形图，雪花，它的原理很简单，就是把一条直线平均分成三段，中间一段是一个等边三角形，然后通过递归吧它做出来得到的就是柯赫曲线，然后改变初始坐标和计算方法，把另外两个柯赫曲线做出来，代码实现如下：
效果如下所示;

1.递归一次：

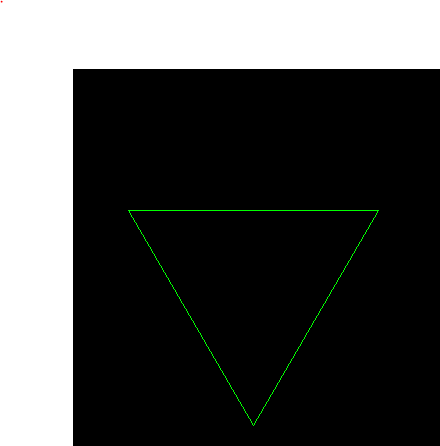
2.递归两次：

/**
* 第一个递归函数，用于画柯赫曲线上部分
*/
public void draw1(double x1, double y1, double x2, double y2, int n) {
g.setColor(new Color(0, 255, 0));
if (n <= 1) {// 退出递归条件
g.drawLine((int) x1, (int) y1, (int) x2, (int) y2);
} else {
// 把x1——>x5作为局部变量，并计算变量
double x3 = (2 * x1 + x2) / 3;
double y3 = (2 * y1 + y2) / 3;
double x4 = (x1 + 2 * x2) / 3;
double y4 = (y1 + 2 * y2) / 3;
double x5 = 0, y5 = 0;
double k = (y4 - y3) / (x4 - x3);
if (y3 == y4) {
x5 = (x3 + x4) / 2;
y5 = y3 - (x4 - x3) * Math.sqrt(3) / 2;
} else {
if (k < 0) {
x5 = x1;
y5 = y4;
}
if (k > 0) {
x5 = x2;
y5 = y3;
}
}

g.setColor(new Color(n, n, n));
draw1(x1, y1, x3, y3, n - 1);
draw1(x3, y3, x5, y5, n - 1);
draw1(x5, y5, x4, y4, n - 1);
draw1(x4, y4, x2, y2, n - 1);
}
}

/**
* 第二个递归函数，用于画柯赫曲线右边
*/
public void draw2(double x1, double y1, double x2, double y2, int n) {
g.setColor(new Color(0, 255, 0));
if (n <= 1) {
g.drawLine((int) x1, (int) y1, (int) x2, (int) y2);
} else {
// 把x1——>x5作为局部变量，计算x1-->x5,y1-》y5
double x3 = (2 * x1 + x2) / 3;
double y3 = (2 * y1 + y2) / 3;
double x4 = (x1 + 2 * x2) / 3;
double y4 = (y1 + 2 * y2) / 3;
double x5 = 0, y5 = 0;
double k = (y4 - y3) / (x4 - x3);
if (y3 == y4) {
x5 = (x3 + x4) / 2;
y5 = y3 + (x4 - x3) * Math.sqrt(3) / 2;
} else {
if (k < 0) {
x5 = x2;
y5 = y3;
}
if (k > 0) {
x5 = x1;
y5 = y4;
}
}
draw2(x1, y1, x3, y3, n - 1);
draw2(x3, y3, x5, y5, n - 1);
draw2(x5, y5, x4, y4, n - 1);
draw2(x4, y4, x2, y2, n - 1);
}
}

/**
* 第三个递归函数画柯赫曲线左边
*
*/
public void draw3(double x1, double y1, double x2, double y2, int n) {
g.setColor(new Color(0, 255, 0));
if (n <= 1) {

g.drawLine((int) x1, (int) y1, (int) x2, (int) y2);
} else {
// 把x1——>x5作为局部变量
double x3 = (2 * x1 + x2) / 3;
double y3 = (2 * y1 + y2) / 3;
double x4 = (x1 + 2 * x2) / 3;
double y4 = (y1 + 2 * y2) / 3;
double x5 = 0, y5 = 0;
double k = (y4 - y3) / (x4 - x3);
if (y3 == y4) {
x5 = (x3 + x4) / 2;
y5 = y3 - (x4 - x3) * Math.sqrt(3) / 2;
} else {
if (k < 0) {
x5 = x1;
y5 = y4;
}
if (k > 0) {
x5 = x2;
y5 = y3;
}
}
draw3(x1, y1, x3, y3, n - 1);
draw3(x3, y3, x5, y5, n - 1);
draw3(x5, y5, x4, y4, n - 1);
draw3(x4, y4, x2, y2, n - 1);
}
}
二、接下来画的是是几棵竹子，它的实现是通过在一条直线上不断出现分支,然后递归就可以得到竹子，代码及效果图如下：

1.递归一次

2.递归两次

public void tree(double x1, double y1, double x2, double y2, int n,
Graphics g) {
if (n >= 1) {
double x3, x4, y3, y4;
// g.drawString("I believe !",0,300);
g.setColor(Color.green);
g.drawLine((int) (x1), (int) (y1), (int) (x2), (int) (y2));
x3 = (x1 + x2) / 2;
y3 = (y1 + y2) / 2;
tree(x1, y1, x3, y3, n - 1, g);
tree(x3, y3, x2, y2, n - 1, g);
x4 = (x2 + y2 - y3 - x3) * 0.7071 + x3;
y4 = (y2 - x2 + x3 - y3) * 0.7071 + y3;
tree(x3, y3, x4, y4, n - 1, g);
x3 = (x1 * 3 + x2) / 4;
y3 = (y1 * 3 + y2) / 4;

x2 = (x2 * 3 + x1) / 4;
y2 = (y2 * 3 + y1) / 4;
x4 = (x2 * 1.732 - y2 + 2 * x3 - x3 * 1.732 + y3) / 2;
y4 = (x2 + y2 * 1.732 - x3 + 2 * y3 - 1.732 * y3) / 2;
tree(x3, y3, x4, y4, n - 1, g);

}

}
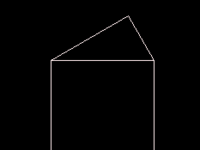
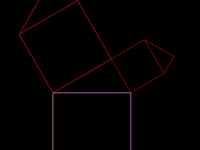
三、毕达哥拉斯树的实现，首先，通过第一点把其余的四点计算出来，再把计算得到的点进行递归，这个计算有点复杂，好坑爹，代码及效果如下：

1.递归一次

2.递归两次

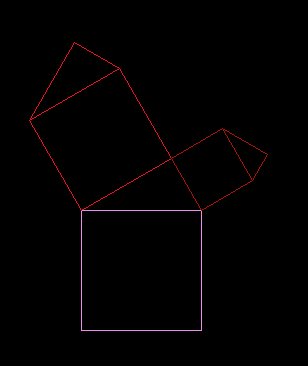
public void draw5(double x1, double y1, double L, double a, double b,
double c, int n) {
double x2;
double y2;
double x3;
double y3;
double x4;
double y4;
double x5;
double y5;
if (n < 1) {// 判断是否继续进行递归调用，注意：判断一定要放在递归调用之前，否则这段代码将永远不会被执行
return;
}
// 计算五个点的位置，以右下点为（X0，Y0）
x2 = x1 - L * Math.sin(a);
y2 = y1 - L * Math.cos(a);
x3 = x2 + L * Math.cos(Math.PI / 6) * Math.cos(a + Math.PI / 6);
y3 = y2 - L * Math.cos(Math.PI / 6) * Math.sin(a + Math.PI / 6);
x4 = x2 + L * Math.cos(a);
y4 = y2 - L * Math.sin(a);
x5 = x1 + L * Math.cos(a);
y5 = y1 - L * Math.sin(a);
Random r = new Random();
int R = r.nextInt(256);
int G = r.nextInt(256);
int B = r.nextInt(256);
g.setColor(new Color(R, G, B));
g.drawLine((int) x1, (int) y1, (int) x2, (int) y2);
g.drawLine((int) x2, (int) y2, (int) x3, (int) y3);
g.drawLine((int) x3, (int) y3, (int) x4, (int) y4);
g.drawLine((int) x4, (int) y4, (int) x2, (int) y2);
g.drawLine((int) x4, (int) y4, (int) x5, (int) y5);
g.drawLine((int) x5, (int) y5, (int) x1, (int) y1);
// 划线——注意方法所需要的数据类型
draw5(x2, y2, L * Math.cos(Math.PI / 6), a + Math.PI / 6, b + Math.PI
/ 6, 0, n - 1);
draw5(x3, y3, L * Math.sin(Math.PI / 6), a - Math.PI / 3, b - Math.PI
/ 3, 0, n - 1);

// 进行递归调用（注意传到方法里的点是相对于新正方形的右下点）
}
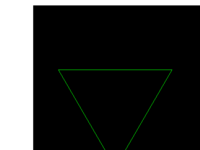
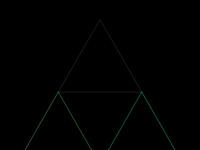
四、谢宾斯基三角形，这个比较简单，就不多说了，代码及效果如下：

1、递归一次

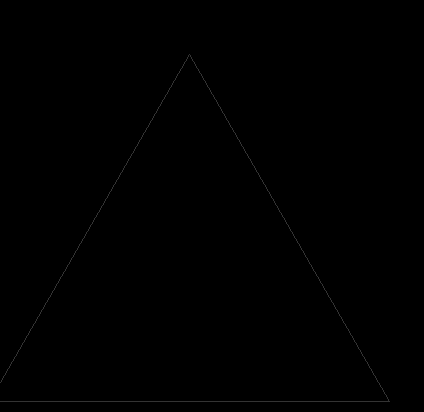
2、递归两次

public void draw6(double x1, double y1, double x2, double y2, double x3,
double y3, int n) {
// （x1,y1）,（x2,y2）（x3,y3)分别表示三角形的三个坐标
if (n <= 0) {// 跳出递归条件
return;

}
Random r = new Random();
int R = r.nextInt(256);
int G = r.nextInt(256);
int B = r.nextInt(256);
// (x4,y4),(x5,y5),(x6,y6)分别表示三角形的三边中点
double x4 = (x1 + x3) / 2;
double y4 = (y1 + y3) / 2;
double x5 = (x1 + x2) / 2;
double y5 = (y1 + y2) / 2;
double x6 = (x2 + x3) / 2;
double y6 = (y2 + y3) / 2;

g.drawLine((int) x1, (int) y1, (int) x2, (int) y2);
g.drawLine((int) x1, (int) y1, (int) x3, (int) y3);
g.drawLine((int) x3, (int) y3, (int) x2, (int) y2);
draw6(x4, y4, x3, y3, x6, y6, n - 1);
draw6(x4, y4, x5, y5, x1, y1, n - 1);
draw6(x2, y2, x5, y5, x6, y6, n - 1);
g.setColor(new Color(R, G, B));

}

五、迷宫，这是我自己给它起的名字，因为不知道这玩意叫什么名字，就胡乱起了个名字，代码及效果图如下：

1、递归一次

2、递归两次

public void draw7(double x1, double y1, double x2, double y2, int n) {
// （x1,y1）,（x2,y2）（x3,y3)分别表示三角形的三个坐标
if (n <= 0) {// 跳出递归条件
return;

}
Random r = new Random();
int R = r.nextInt(256);
int G = r.nextInt(256);
int B = r.nextInt(256);
// (x4,y4),(x5,y5),(x6,y6)分别表示三角形的三边中点
double x3 = x1 + (x2 - x1) / 3;
double y3 = y1 + (y2 - y1) / 3;
double x4 = x2 - (x2 - x1) / 3;
double y4 = y2 - (y2 - y1) / 3;
g.draw3DRect((int) x1, (int) y1, (int) x2 - (int) x1, (int) y2
- (int) y1, false);
g.draw3DRect((int) (x1 + (x2 - x1) / 3), (int) (y1 + (y2 - y1) / 3),
(int) (x2 - (x2 - x1) / 3) - (int) (x1 + (x2 - x1) / 3),
(int) (y2 - (y2 - y1) / 3) - (int) (y1 + (y2 - y1) / 3), true);

// 画对角部分
draw7(x1, y1, x3, y3, n - 1);
draw7(x4, y4, x2, y2, n - 1);
draw7(x4, y1, x2, y3, n - 1);
draw7(x1, y4, x3, y2, n - 1);
// 画四面部分
draw7(x3, y1, x4, y3, n - 1);
draw7(x1, y3, x3, y4, n - 1);
draw7(x4, y3, x2, y4, n - 1);
draw7(x3, y4, x4, y2, n - 1);
g.setColor(new Color(R, G, B));

}

六、无穷圆，代码实现及效果如下如下：

1、递归一次

2、递归两次

public void draw8(double x1, double y1, double x2, double y2, int n) {
// （x1,y1）,（x2,y2）（x3,y3)分别表示三角形的三个坐标
if (n <= 0) {// 跳出递归条件
return;

}
Random r = new Random();
int R = r.nextInt(256);
int G = r.nextInt(256);
int B = r.nextInt(256);
// (x3,y3),(x4,y4),(x5,y5),(x6,y6)分别表示圆的起始和终点坐标
double x3 = x1;
double y3 = y1;
double x4 = (x2 + x1) / 2;
double y4 = y1;
double x5 = (x2 + x1) / 2;
double y5 = y1;
double x6 = x2;
double y6 = y2;
g.drawOval((int) x1, (int) (y1 - (x2 - x1) / 2), (int) (x2 - x1),
(int) (y2 + (x2 - x1) / 2 - y1 + (x2 - x1) / 2));
draw8(x3, y3, x4, y4, n - 1);
draw8(x5, y5, x6, y6, n - 1);
g.setColor(new Color(R, G, B));

}
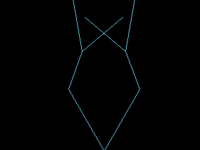
七、树，代码及效果图如下：

1、递归一次

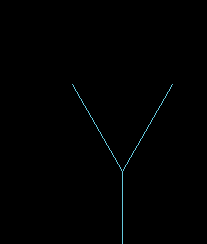
2、递归两次

public void draw9(double x0, double y0, double a, double b, double L, int n) {

if (n == 0) {
return;
}
double x1 = x0 + L * Math.cos(a) / 2;
double y1 = y0 - L * Math.sin(a) / 2;
double x2 = x1 - 2 * L * Math.cos(5 * Math.PI / 6 - a) / 3;
double y2 = y1 - 2 * L * Math.sin(5 * Math.PI / 6 - a) / 3;
double x3 = x1 + 2 * L * Math.cos(a - Math.PI / 6) / 3;
double y3 = y1 - 2 * L * Math.sin(a - Math.PI / 6) / 3;
g.setColor(new Color(100, 200, 220));
g.drawLine((int) x0, (int) y0, (int) x1, (int) y1);
g.drawLine((int) x1, (int) y1, (int) x2, (int) y2);
g.drawLine((int) x1, (int) y1, (int) x3, (int) y3);
draw9(x2, y2, a + b, b, 3 * L / 4, n - 1);
draw9(x3, y3, a - b, b, 3 * L / 4, n - 1);
}

美丽的分形.zip (231.1 KB)
下载次数: 0